站在巨人的肩膀上

♪ 声子色散曲线

感谢台湾科技大学宫非博士对声子色散曲线(PDC)的讲解。原文见此处

感谢博主manmanaa在CSDN中的博文，讲解了PDOS和PDC的联系。原文见此处

• PDOS 可以理解为体系内原子的分布概率(宏观角度)，也可以理解为声子处于某种状态的概率（量子力学角度）。

• PDC 是频率和波矢的关系函数。对于一个晶胞内含有N个独特原子的体系，其色散关系曲线一个有3N个分支，其中3个声学枝，3(N-1)个光学支。

如下图a典型石墨烯色散曲线所示，在单层石墨烯的一个原胞中包含有两个不等价的碳原子A和B。因此，对于单层石墨烯来说，总共有六支声子色散曲线，分别为三个光学支 (面内光学纵波 iLO、面内光学横波iTO和面外光学横波oTO)和三个声学支(面内声学纵波iLA、面内声学横波iTA和面外声学横波oTA)。面内(i)和面外(o)分别为原子的振动方向平行或者垂直于石墨烯平面，纵向(L)和横向 (T)即为原子的振动方向平行或者垂直于A-B碳碳键的方向。图b为514.5nm激光激发下单层石墨烯的典型拉曼光谱图。单层石墨烯有两个典型的拉曼特征，分别为位于$1,582cm^-1$附近的G峰和位于$2,700cm^-1$左右的G' 峰，而对于含有缺陷的石墨烯样品或者在石墨烯的边缘处，还会出现位于$1,350cm^-1$左右的缺陷D峰，以及位于$1,620cm^-1$附近的D'峰。图c 给出了石墨烯各个拉曼特征峰的产生过程，入射激光作用下，石墨烯价带上的电子跃迁到导带上，电子与声子相互作用发生散射，从而可以产生不同的拉曼特征峰。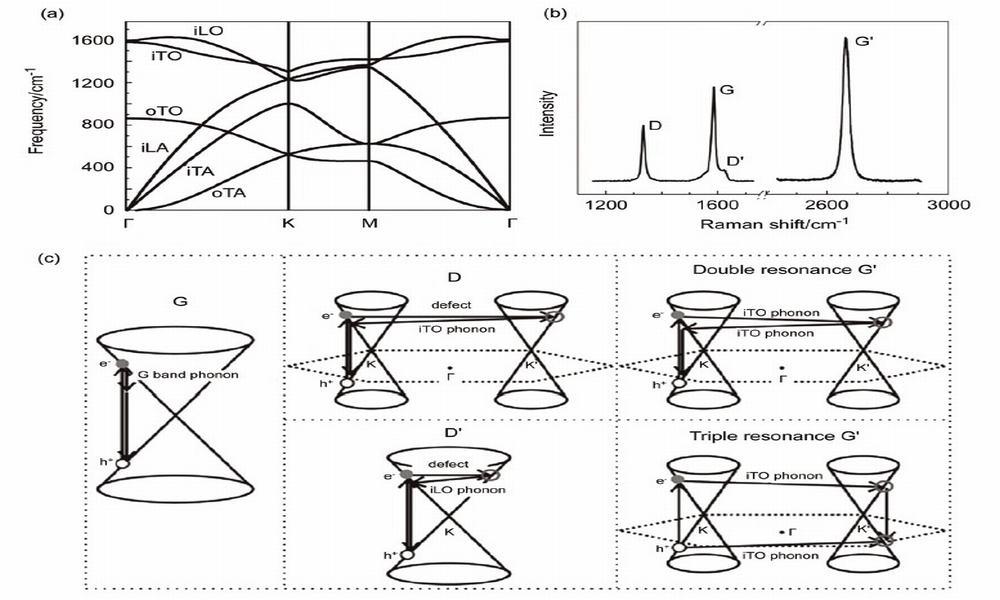

• 色散关系一个重要的应用是用来得到群速度以及色散曲线的斜率。$v_g%$$$v_g={\left({ \frac{dω}{dK} }\right)}$$

典型声子色散图片,可见北京大学高鹏教授于2021年11月发表在《Nature》中的《Measuring phonon dispersion at an interface》。利用four-dimensional electron energy-loss spectroscopy(四维电子能谱技术)，直接测量了外延立方氮化硼/金刚石异质界面的局部振动谱和界面声子色散关系。见下图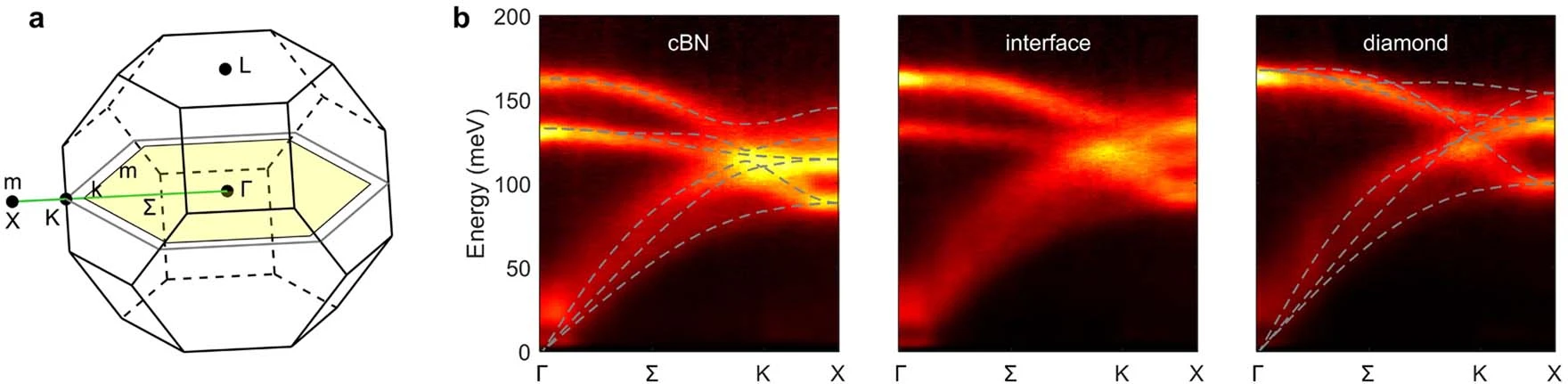

PDOS和PDC的关系

以上为六方氮化硼的声子色散曲线，曲线上的每一个点都代表一种声子模，统计一下以上点的概率分布，与PDOS相比较，可以看到，两者的形状神相似。理论上，如果体系足够大，声子模足够多，这两个曲线应该是重合的。

---